An Engineering Guide to Bicycle Wheel Balancing

Introduction
Bicycle wheel balancing is a topic that is often discussed but has not ever been dissected in detail. A lot of professionals balance their wheels and this has filtered down to the amateur ranks wishing to eek out the maximum amount of performance. This post will look at the engineering behind the balancing of bicycle wheels.
Types of Imbalance (Static and Dynamic)
There are two fundamental modes of balancing. Static and Dynamic.
Dynamic Balance
The most common type that people will have come across and the most obvious will be dynamic balancing, this occurs when car wheels are balanced. A car wheel doesn’t have a particularly large diameter in comparison to it’s axial length so it is not considered to be a slender body (thin). Hence balancing must occur on two planes, the first is near the outer edge of the wheel and the second is towards the inner edge of the wheel. This is depicted below in the diagram with the orange rectangles representing counterweights. It should be noted that almost every industrial machine that rotates has some basic balancing carried out on it.
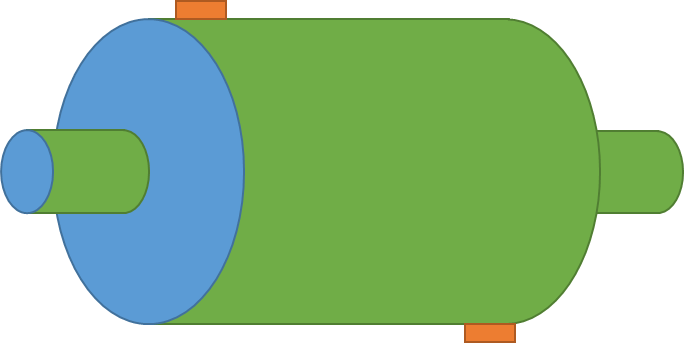
A dynamic balance is technically difficult to perform without the correct hardware as it requires phase angle measurement (more below) to determine the position of the weight.
Static Balance (Bike Wheels)
A static balance is used primarily for slender objects, those that have a high diameter to to thickness ratio. Depending on the text, the ratio for slenderness varies but is generally of the order of 5:1. In the case of a bike wheel, this comfortably exceeds this ratio (typically over 6:1). A static balance is considerably easier to perform as only one balance weight needs to be applied for correction and is therefore often called a single plane balance.

Causes of Imbalance
The primary causes of imbalance are due to physical properties such as valves but a large element is due to imperfect manufacturing techniques.
- Valve Hole
- Tire
- Tube
- Excess resin build up (carbon wheels are frequently made in quadrants)
- Non uniform layup
- Deviations in material density
- Out of True
Typically, a wheel will have it’s light spot (when it is not assembled) at the valve hole because there is physically less material there. Once built up, this light spot will usually become the heavy spot due to the weight of the tire valve. Poorly manufactured wheels will often have a significant phase angle difference (see more below).
Symptoms of Imbalance
Imbalance causes a number of symptoms that often overlap other issues
- Speed Wobble
- Road Buzz
- Brake Pulsing
- Broken Spokes
- Poor Bearing Life
Acceptable levels of imbalance (Balance Tolerance)
Rotor balancing is covered in an ISO technical standard 21940 Section 11 which documents vibration and mechanical rotor balancing grades. This ISO standard is used for everything from Jet Engines to Hard disk drives and is widely accepted as a definitive standard. Variations of it can be traced back to pre 1900’s.
A bicycle wheel is by definition a slender object. The diameter is much larger than it’s axial length. The diameter being 700mm+ vs an axial length of approximately 130mm and in reality, the portion carrying the weight at that diameter is only around 30mm thick. Thus a static or single plane balance can be used to correct imbalance.
The generic formula for imbalance is
\begin{equation} imbalance (g \cdot mm) = \frac {9549 \cdot G \cdot RotorMass(kg)} {RotorSpeed (RPM)} \end{equation}The key parameters that are left for user choice are the speed and also the G rating. The speed is self explanatory and should be considered to be the maximum velocity that you intend to ride at. The parameter G or the balance grade is a contentious subject in engineering circles as to what is an appropriate grade. As a comparison, a car wheel is typically balanced to 40, A computer hard drive is balanced to 0.6. G6.3 is a common balancing tolerance that is used for a variety of machinery and is the standard that is recommended in this text for absolute performance, for most a tolerance standard of G40 would be acceptable.
Making a few assumptions, such as the rolling circumference of the wheel and tire combination is 2.1m, wheel mass of 0.8kg and a balance grade of G40, the formula becomes. Note: The wheel mass must include all elements of the rotating assembly, eg cassette, tires, tubes.
\begin{equation} imbalance ( g \cdot mm) = \frac {48120 \cdot WheelMass(kg)} {Speed(kph)} \end{equation}If the numbers are plugged in for a typical wheelset, mass of 0.8kg and speed of 40km/h. The permissible imbalance becomes
\begin{equation} 962 g mm = \frac {48120 \cdot 0.8} {40} \end{equation}To make this relatable to a physical mass, divide through by 311mm. This is the approximate radial distance to the rim periphery and is half of 622mm.
\begin{equation} 3 g = \frac {962gmm } {311mm} \end{equation}Equation (2) can thus be simplified into one line for a balance weight
\begin{equation} BalanceWeight _{rimouter} ( g ) = \frac {154.7 \cdot WheelMass(kg)} {Speed(kph)} \end{equation}The calculated balance weight is based on a radial distance of 311mm. In most situations, weight is applied at a slightly shorter radial distance and hence a greater weight must be applied.
Some key points to note, the Permissible imbalance becomes smaller in the following conditions :
- The wheelset becomes lighter (typically a front wheel will require a tighter tolerance than a rear wheel)
- The bicycle velocity and hence the rotational speed of the wheel increases
A graph below is shown for differing weights of wheel assemblies against speed. The Y axis is the balance limit weight based on equation (5). This is intended as a rough guide but should prove to be accurate in most scenarios.
Phase Angle
The phase of the out of balance and the corresponding movement of the wheel are of importance. In perfect conditions, the wheel orbit lags the out of balance by 90 degrees. This is due to maximal acceleration always being perpendicular to the out of balance. See the graph below. It is recommended that this video is watched to explain this in greater depth.
In a purely theoretical situation, an exactly matching counterweight will cancel the sine wave produced by the out of balance but this is rarely achievable in a practical situation. Realistically, a counter weight will be of a slightly heavier and positioned at a radius slightly inwards of the wheel rim. Additionally, it is extremely unlikely the counter weight will be positioned at the perfect angle. The net result is a waveform that tends towards zero but does not quite cancel out.
The drawing below shows the out of balance weight denoted by the orange out of balance, and the gray correction weight that is mounted slightly inwards and at a slightly imperfect phase angle. This is an attempt to model real life more accurately.

The waveforms for exact corrections and the imperfect correction are shown below. Essentially the phase angle is slightly off and the mass is slightly smaller.
The finalized waveform is shown below. The aim would be for a net zero but despite this it is a significant improvement and would be easily noticeable when riding.
In most scenarios this will be perfectly adequate and a vast improvement but in other situations the natural frequency of the assembly can be shifted such that the wheel will behave erratically – this is extremely rare and (at the time of writing) undocumented in bicycle wheels but it could potentially cause exacerbated speed wobbles .
Critical Speeds
A critical speed occurs when the driver frequency and a natural frequency of the object are equal or very close to each other. This is best practically shown by the video below, This wheel was original at a speed above it’s critical (there is usually more than one critical speed) and then slowed to it’s critical at which point the entire bike vibrated violently and then exited it’s critical speed. Once exiting it’s critical speed, the vibration decayed. In the case of this wheel, one of the critical speeds was 42 Km/h.
Performance aspects of Imbalance
The power loss from an out of balance wheel comes from having to accelerate the mass around it’s eccentric orbit. This power loss is greatly effected by a number of factors – rotational speed, natural frequency, wheel mass, out of balance mass.
It is not possible to give an exact power loss figure for every situation but the graph below shows a hypothetical situation. A 1.8kg assembled wheel, 20g, 15g, 1g out of balance and a rotational speed within the resonance range of 46km/h.
Many could argue this is a “doomsday” scenario as resonance does increase the power loss considerably but it is important to note the natural frequency of many bike wheel assemblies sits comfortably within the range of a lot of time trial riders.
Rectifying Imbalance and when to rectify
Rectification of imbalance is technically straightforward, a corrective balance weight is placed on the opposite side to the heavy spot. In practice the application of this weight and it’s position pose some potential problems.
The biggest issue is often the aerodynamic penalty. A weight is often cumbersome and does not lend itself well to the trailing edge of bike rims. A solution to this is to place the weight inside the spoke holes, a practice that is often used by pro-riders. This practice is much easier with rims that have the rear end of the nipples exposed as opposed to those rims which have a flat bed. The most common counterweight measures are
- Golf Club Weights (Tungsten or Lead)
- Lead Tape
- Machined plugs to go into the spoke holes
In general terms, the reasons for rectifying imbalance would be necessary when the following are considered
- Minimization of power losses in the drive train
- Imbalance over 10g at the wheel periphery
- Speed 35-40km/h+
- Lightweight rider (it is more beneficial to balance the front wheel)
- Lightweight wheels (it is more beneficial to balance the front wheel)
- Road Buzz
- Poor Bearing Life
- Speed Wobbles
Watch on YouTube
This topic is somewhat complex and watching the video below is recommended as it explains some of these concepts with practical results.





The power dissipation part feels wrong to me. You say “power loss from an out of balance wheel comes from having to accelerate the mass around it’s eccentric orbit” but that’s just not true. In theory it takes 0 more watts to spin an imbalanced wheel than a balanced one. I’m not sure where the disconnect is but I suspect the key missing insight is that the force necessary to induce the wobbly motion in an out-of-balance wheel is perpendicular to the motion of the CG and therefore no ‘work’ is performed and no energy lost. Think of a sun (like an axle) with two equal planets orbiting directly each other–the sun doesn’t move at all, cool. Now imagine we remove one planet for a completely ‘out of balanced system’. The sun now wobbles around from the imbalance, but there is no energy dissipated in either system; they both orbit forever. Now there *are* higher order effects like extra loads on bearings, damping of motions induced in not-perfectly-stiff support materials, etc. but these are likely tiny effects measured in milliwatts.
The crux of this is the loss from the various parts that are flexing, Energy is absorbed there. It gets much worse when it resonates. There is a whole section in the book called RotorDynamics by an ex bently nevada engineer Agnes Muzinska. She talks about it in full Eigenvector terms – there is a stiffness matrix for each of the constituent parts and then the displacement and subsequent energy loss associated with them. It’s too much for this post.
Thanks for the reply and for the blogs and videos.
Sounds like we agree that any losses would be coming from damping of flexing in the system (and certainly these losses will be highest around resonance.) I think the big questions is how big are those losses in the real world. My (somewhat educated) estimate from doing a bunch of rough math is that the losses would be low from normal wheel imbalance (way under a watt) in any realistic riding situation. But, if they are higher than this (e.g. 5-20 watts as you show in the graph) they would represent a *massive* component in the bike optimization equation. If balancing wheels could save even 2-3 watts, that would be revolutionary. It would be great to get to the bottom of this!
Do you really think there are important (>1/2 watt, say) power losses coming from something like a 5 gram imbalance in a wheel in a normal riding scenario?
When your loaded wheel that is accelerated with 1G down to earth force with you riding it “with its mass out of orbit, no matter its looking ‘straight going’ ” than your mass takes a longer distance for the same route, that requires more watts to move the load the same road with the same wheel.
Its the same problem when your rim is bent / goes visible in shape out of orbit. Even if it is only 2mm that the wheel is going left right left right, it goes with aero-penalty but also the moves a longer distance… it requires less power to move that same way when its absolutely straight spinning.
With the mass beiing unbalanced turns out exactly the same… the mass behaves like if the wheel is not straight, like if it has a radial runout.
Wie ein Höhenschlag im Ventilbereich halt, bei höheren Geschwindigkeiten merkst du das, weil das Rad unrund läuft und Energie an den Rahmen abgeben will, es fängt an zu vibrieren und hoch und runter zu schlagen bei jeder Umdrehung… das kostet Energie, auch beim fahren, fühlt sich an wie Kopfsteinpflaster plötzlich bei hoher Geschwindigkeit, ungeil! Wir sind nicht in der Schwerlosigkeit und ich weiß die Sonne ist riesig, aber im Vergleich dazu ist die Masse deines Fahrrad zur Erde doch eher verschwindend gering. Die Erde wobbled nicht weil du mit 100kg irgendwo rumfährst. Völlig abstruser Vergleich!
Hello Dave Rosenthal, My name is Dan Sotelo, And yes unbalanced bicycle wheels do have a very detrimental effect on overall performance. Here’s how.
It starts with Newton’s First Law… A mass that is put in motion will continue in motion unless it is interrupted by an OUTSIDE FORCE (i.e. Air Drag etc), or an OSCILLATION (i.e. Wheel Balance etc).
EXAMPLE: An unbalanced wheel by as little as 8 grams causes a chain of detrimental effects as speeds pick up say 25 ~ 50+ MPH, like descending mountain roads.
1. High speeds centrifugal forces / G-forces increase on the unbalanced 8 grams then start to convert the 8 grams into ounces. There are 28.35 grams in one-ounce and I did the research and found that at 40 mph the G-forces are about 6~8 Gs on a 700c wheel. Which increases the weight of the 8 grams x 6 to 8 times heavier.
2. At about 25 ~ 35 mph the wheel that is off balance by 8 grams is now off balanced by 2 ~ 3 ounces! This now causes powerful oscillation forces, which start to invite the entire weight of the wheel to also start oscillating, from the axle to the outer perimeter of the tire! (FYI: Rear wheel weight is o/a 1.4 lb and front wheel weight is o/a 1.2 lb.) But because bicycles are designed to absorb vibrations the rider dose not feel much at this point.
3. But as speeds pick up (35 ~ 50+ mph) you will start to notice that the bike starts to handle nervously, that’s because now the wheels starts to act like a 1.4 lb sledgehammer swinging off your rear axle and a 1.2 lb sledgehammer swinging off your front axle..!
4. Here’s where the chain of events gets even worse…. As the front and rear wheels spin and oscillate at high speed the powerful spinning 1.4 & 1.2 lb oscillation forces start to go in and out of synchronization. But when they do get in sync, now you have a 2.6 lb sledgehammer swinging off your axles!!! This is when bikes start to experience High Speed Wobble!
Other detrimental effects caused by unbalanced wheels at any speed is because they cause “Interrupted Inertia”. If a wheel is perfectly balanced it carries “Smooth Flowing Inertia” which increases performance by greatly improving rolling efficiency, and handling, especially at high speeds. Often making an ill handling bike to feel like it’s on rails!
So yes, balanced wheels greatly improve performance & SAFETY at high speeds, even more so than Aerodynamics alone.
For my background Google Dan Sotelo onZa
In terms of a simple balancing solution Silca has a product called “speedbalance”, what do you think the aero penalty is for something like this?
https://silca.cc/collections/tubeless/products/speedbalance-wheel-balancing-and-computer-magnet-syste
They also use something similar for their tubeless valves and clame it saves 0.5 watt (at 30 mph) compared to a standard valve.
https://silca.cc/collections/tubeless/products/tubeless-valve-kit-w-speedshield
What do you think of the solution?
You are better off if you can to put the weight in the spoke holes, sticking a rather hefty lump on the trailing edge of the wheel will influence the aerodynamics quite a lot. If they are quoting 0.5W, I hate to think how much the aerodynamic loss is.
Okay thx for the reply!
Balanced an old set of Zipp 404s a couple months back, front and rear needed around 12-15 grams each and they feel faster. Just got a new bike with ENVE 7.8 wheels and they were also off by around that much. Just balanced them. Note to manufacturers: If I have to balance the wheels, I’m peeling your logos off my wheels. Added 24 grams to my ENVE wheels, but removed 13 grams of stickers. Didn’t measure the Zipp decals, but I think they were heavier.
http://ambrosiowheels.com/en/rims/classics/nemesis/ have a weight added at the valve hole to balance them, contrary to “… a wheel will have it’s light spot (when it is not assembled) at the valve hole because there is physically less material there. Once built up, this light spot will usually become the heavy spot due to the weight of the tire valve. ”
While the bouncing bikes on workstands is a great video, I doubt wheel balance really makes much difference at road speeds on roads. I’ve moved wheel sensors around to make front wheels more “balanced” over the years but can’t really think of a time when I really noticed any difference, even at higher speeds.
So its quite simple. Check your valves weight, mine 2x TUNE 35mm Aluminum plus Aluminium Caps each ~4,5g minus ~0,5g for the valve hole = 4g. The easiest solution is spoke reflective-clips. Each weight is 0,9-1g… so its ~4 pieces for me on each wheel and they are balanced down to <1g in 5 seconds. "Clip On & Done."
Yeah the spoke-reflective-clips come with a little aero-penalty. Well, but regarding 4 pieces only on 2 spokes, according to hambini the gain from balacing should be higher. 😉
In my experience, a better visualisation is to consider that an unbalanced wheel has the center of gravity (CoG) displaced from the axle, thus if the wheel was able to spin in space it would spin about the centre of gravity, and the axle (when viewed from the side) would describe an orbit around the CoG. The purpose of balancing is to reduce the diameter of this orbit, ideally to zero. In the case of hydro machines with journal bearings – which I have been involved in balancing – the aim is to reduce this orbit to within the diametric clearance of the bearing (these are machines of tens of tons, with diameters of 5m or more, and bearing clearances measured in thousands of an inch) . If an unbalanced wheel is made to spin fast enough, it will rotate about the CoG, regardless of restraints, although vibration would be increasing with speed of rotation. This may not be evident at slow speeds due to the smaller forces involved, and the damping/mass of the system of tyres, forks/wheel elasticity (springiness) and rider mass. Is it important? Well, it depends – on the resonant frequencies of the bike, which may affect steering and handling. Just as a repeated small push at the right time gets a child on swing moving with great speed, a system being excited at the resonant (or critical) frequency keeps adding a portion of the energy of the exciting force until a balance is reached (the resonant peak) – so even a small excition force can build up large vibrations given enough time and the right conditions. While every system has resonant frequencies, if there isn’t an exciting energy source, it doesn’t matter – hence the desirablibilty of balancing the wheels. Apart from the bike, there are nowadays other things that might not like vibrations, eg bike computers, phones and so on – it takes me about 15 mins to do a static balance on a bike wheel, it seems like a no brainer to me.
How would you balance a tubeless setup? The sealant will naturally pool at the bottom.
Great article! This is a topic unknown to many bike shops in my area. However, I have a bit off-topic question. On “Extreme Wheel Resonance” video while a rear wheel is spinning, cranks are still. However in my bike they are rotating a bit. I was asking local mechanic about it and he says it fine, but I am not convinced. Could you explain what could be reason for that? Drag in bottom bracket or rear wheel bearings? Thanks!